Lettre 41 - Spinoza à Jarig Jelles (5 septembre 1669)

à Monsieur Jarig Jelles,
B. de Spinoza.

Monsieur,

Je vous rapporterai en quelques mots l’expérience sur laquelle vous m’avez questionné d’abord de vive voix, puis par lettre. A ce récit je joindrai l’énoncé de mon opinion présente sur ce sujet.

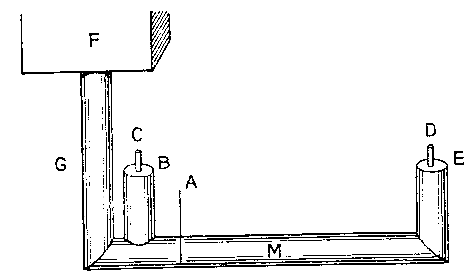
J’ai fait fabriquer un tube de bois de dix pieds de long, large à l’intérieur d’un pouce et demi, et j’y ai adapté trois tubes perpendiculaires comme le montre la figure ci-jointe. Pour éprouver en premier lieu si la pression de l’eau était la même dans le tube B que dans le tube E, j’ai bouché le tube M en A au moyen d’une tige préparée à cet effet. Ensuite j’ai rétréci l’orifice du tube B de façon qu’il laissât juste passer un tube de verre C. Après avoir à l’aide du vase F rempli d’eau mon appareil, j’ai noté à quelle hauteur le liquide s’élevait dans le tube C. Ensuite j’ai fermé le tube B, et, en levant la tige A, je laissai l’eau couler jusqu’à ce qu’elle parvînt dans le tube E arrangé de même façon que le tube B. Remplissant alors d’eau l’appareil, je constatai que l’eau montait en D à la même hauteur que précédemment en C ; j’en ai conclu que la longueur du tube n’était pas un obstacle ou n’en était qu’un minime. Pour le voir avec le plus de précision j’ai voulu expérimenter si le tube E pouvait remplir un pied cube préparé à cet effet en aussi peu de temps que le tube B.

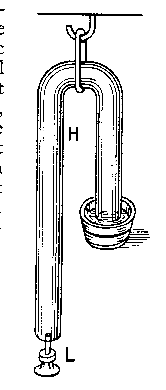
N’ayant pas sous la main de pendule pour mesurer le temps, je me suis servi d’un tube de verre courbé tel que H, dont la branche la plus courte était plongée dans l’eau, tandis que la branche la plus longue s’ouvrait à l’air libre. Après ces préparatifs j’ai fait couler en premier lieu de l’eau par le tube B, le jet étant de la grosseur du tube lui-même, jusqu’à ce qu’un pied cube fût rempli. Alors avec une balance précise j’ai mesuré quel poids d’eau avait coulé dans le petit récipient L pendant le même temps, et j’ai trouvé qu’il y en avait quatre onces. Fermant alors le tube B, j’ai fait couler de l’eau de façon à remplir un pied cube par le tube E, le jet étant toujours de la grosseur du tube. J’ai pesé, comme je l’avais fait auparavant, l’eau qui avait coulé pendant ce temps dans le récipient L, et j’ai constaté que le poids de cette eau ne dépassait même pas d’une demi-once le poids recueilli précédemment. Comme toutefois le jet n’avait pas été constamment de même force tant en B qu’en E, j’ai recommencé l’opération après avoir apporté, pour l’avoir sous la main, autant d’eau que la première expérience m’avait montré qu’il en fallait. Nous étions trois à opérer, attentifs autant que possible à faire avec plus de précision l’expérience relatée ci-dessus ; nous n’avons cependant pas réussi à la faire avec autant de précision que je le souhaitais. Je pense néanmoins être suffisamment renseigné pour conclure, puisque j’ai trouvé à peu près la même différence de poids dans les deux cas. Tout bien examiné, je suis obligé de croire que la longueur du tube n’a d’effet qu’au début quand l’eau commence à couler. Mais après peu de temps elle coule avec la même force par un tube très long que par un court. La raison en est que la pression de l’eau située au-dessus conserve toujours la même force et récupère constamment par sa pesanteur tout le mouvement qu’elle communique. Elle communiquera donc toujours ce mouvement à l’eau contenue dans le tube jusqu’à ce que l’eau poussée en avant ait acquis autant de vitesse que l’eau située au-dessus peut lui attribuer de force en vertu de la pesanteur.

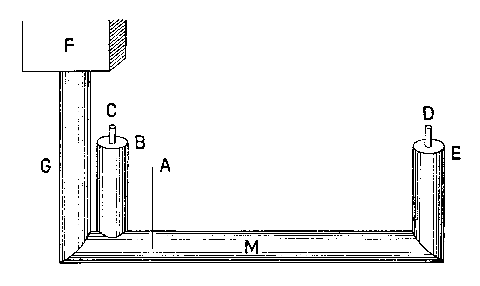
Il est certain que si l’eau contenue dans le tube G confère dans le premier instant à l’eau du tube M un degré de vitesse, dans le deuxième instant, si elle conserve la même force, elle lui communiquera quatre degrés de vitesse, et ainsi de suite jusqu’à ce que l’eau contenue dans le long tube M ait exactement autant de force que, par sa pesanteur, l’eau contenue dans le tube G peut lui en communiquer. De sorte qu’au bout d’un court laps de temps, l’eau coulant par un tube de quarante mille pieds de long acquerra par la seule pression de l’eau située au-dessus autant de vitesse que si le tube M n’avait qu’un pied. J’aurais pu déterminer le temps nécessaire pour que l’eau contenue dans un tube plus long atteigne cette vitesse, si j’avais disposé d’instruments plus parfaits. Cela cependant ne me paraît pas aussi nécessaire, le plus important étant connu, etc.

Voorburg, le 5 septembre 1669.