Lettre 40 - Spinoza à Jarig Jelles (25 mars 1667)

à Monsieur Jarig Jelles,
B. de Spinoza.

Votre dernière lettre, écrite le 14 de ce mois, m’est parvenue sans retard, mais divers empêchements ne m’ont pas permis d’y répondre plus tôt. J’ai parlé à M. Vossius de cette affaire d’Helvétius ; il a beaucoup ri (je me dispense de relater tout notre entretien) et a même été surpris des questions que je lui posais au sujet de pareilles billevesées [1]. Pour moi, sans me soucier en rien de cet étonnement j’ai été trouver l’orfèvre même qui avait éprouvé l’or et dont le nom est Brechtelt. Ce dernier tint un tout autre langage que M. Vossius et affirma que le poids de l’or s’était accru entre le moment de la fonte et celui de la séparation, qu’il avait augmenté en proportion du poids de l’argent introduit dans le creuset pour effectuer la séparation : d’où il concluait que l’or, celui qui provenait de la transmutation de l’argent, avait quelque propriété particulière. Il n’était pas le seul : diverses autres personnes alors présentes ont fait la même expérience. Après cela je me suis rendu auprès d’Helvétius qui me montra et l’or et le creuset intérieurement revêtu d’or et me raconta qu’il avait mêlé dans le creuset, au plomb fondu, à peine un quart de son poids d’orge ou de graine de moutarde. Il ajouta qu’il publierait bientôt un récit de toute l’affaire et rapporta en outre qu’une certaine personne (celle-là même, prétendait-il, qui était venue le voir) avait fait à Amsterdam la même expérience. Vous en avez certainement entendu parler. Voilà ce que j’ai pu apprendre concernant cette affaire.

L’auteur du petit livre dont vous faites mention (il s’y vante de démontrer que les preuves de l’existence de Dieu données par Descartes dans la troisième méditation et dans la quatrième sont fausses) va certainement livrer combat à son ombre propre et se fera à lui-même plus de tort qu’aux autres. L’axiome de Descartes, je le reconnais, est quelque peu obscur comme vous l’avez observé il aurait donné un énoncé plus clair et plus vrai s’il avait dit : La puissance dont la Pensée dispose pour penser n’est pas plus grande que la puissance dont dispose la nature pour exister et agir. C’est là un axiome clair et vrai d’où il suit que l’existence de Dieu découle très clairement et de façon irréfragable de l’idée de Dieu. L’argumentation de l’auteur ci-dessus visé, que vous examinez, montre assez clairement qu’il n’entend pas le sujet. Il est vrai que par une décomposition en parties comme celle qu’il se propose, on peut aller à l’infini. Si par exemple on demande par quelle cause un corps limité de telle façon déterminée est mû, on peut répondre qu’il est déterminé au mouvement dont il est animé par un autre corps, ce dernier par un troisième et ainsi de suite à l’infini. On est libre de répondre ainsi parce qu’il ne s’agit que du mouvement et que nous lui assignons une cause suffisante et éternelle, en posant que les corps forment une suite continue. Mais si j’aperçois un livre plein de méditations sublimes et d’une belle écriture dans les mains d’un homme du peuple, et si, quand je lui demande d’où il l’a, il me répond qu’il l’a copié sur un autre livre appartenant à un autre homme du peuple qui avait lui aussi une belle écriture et ainsi de suite à l’infini, je ne me tiendrai pas pour satisfait. Ma question en effet ne se rapporte pas seulement à la forme et à l’ordre des lettres, seul point sur lequel il réponde, elle concerne aussi les pensées et la manière de voir qu’expriment les mots. Il ne donne aucune réponse en remontant à l’infini. Pourquoi son raisonnement ne peut s’appliquer aux idées, on le voit facilement par l’axiome 9 tel que je l’ai énoncé dans les Principes de la philosophie de Descartes démontrés géométriquement.

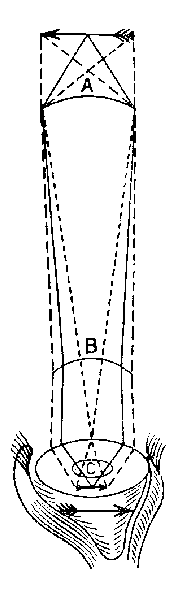
Je vais répondre maintenant à votre deuxième lettre, écrite le 9 mars, où vous me demandez de vous expliquer plus complètement ce que je vous écrivais dans ma dernière lettre au sujet d’une figure circulaire. Vous pourrez aisément me comprendre, si vous voulez bien considérer que tous les rayons que l’on suppose tomber parallèlement sur le verre antérieur de la lunette, ne sont pas réellement parallèles (puisqu’ils sont issus d’un même point) mais sont assimilés à des parallèles parce que l’objet est situé à une distance telle de nous, que le diamètre de la lunette, eu égard à cette distance, se réduit à un point. Il est certain en outre que pour voir un objet en entier nous avons besoin non seulement des rayons qui viennent d’un point unique, mais aussi de tous les cônes de rayons provenant de tous les autres points et qui, par cela même, après avoir traversé le verre, convergent nécessairement en autant de foyers. La structure de l’œil, à la vérité, n’est pas telle que tous les rayons issus de divers points de l’objet convergent rigoureusement en autant de points différents au fond de l’œil, mais il est certain que les figures possédant cette propriété doivent être préférées aux autres. Or un segment de cercle présente ce caractère que tous les rayons issus d’un même point convergent nécessairement en un point situé sur le même diamètre (je l’entends au sens mécanique) et que tous les rayons provenant d’autres points de l’objet se réunissent en autant de points différents. De chacun de ces points en effet on peut mener une ligne qui passe par le centre du cercle ; il faut observer seulement que, si l’on n’avait besoin que d’un foyer unique, l’ouverture de la lunette pourrait être beaucoup plus petite ainsi que vous le verrez sans peine. Ce que j’ai dit ici du cercle, on ne peut le dire de l’ellipse ni de l’hyperbole, et encore bien moins des autres figures plus composées parce qu’on ne peut mener qu’une seule ligne, et d’un seul point de l’objet, qui passe par les deux foyers d’une figure de cette sorte.
Voilà ce que j’ai voulu dire dans ma première lettre.
La figure ci-jointe vous permettra de comprendre comment on démontre que l’angle formé à la surface de l’œil, par les rayons issus de divers points, est plus grand ou plus petit suivant que les foyers sont plus ou moins distants.

Il ne me reste donc plus, après vous avoir envoyé mes meilleures salutations, qu’à me dire, etc...

Voorburg, le 25 mars 1667.